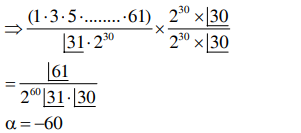Q. Consider the sequence $a_1, a_2, a_3, \ldots \ldots$ such that $a_1=1, a_2=2$ and $a_{n+2}=\frac{2}{a_{n+1}}+a_n$ for $n =1,2,3, \ldots$. If $\left(\frac{a_1+\frac{1}{a_2}}{a_3}\right) \cdot\left(\frac{a_2+\frac{1}{a_3}}{a_4}\right) \cdot\left(\frac{a_3+\frac{1}{a_4}}{a_5}\right) \cdot \cdots \cdot\left(\frac{a_{30}+\frac{1}{a_{31}}}{a_{32}}\right)=2^a\left({ }^{61} C_{31}\right)$, then $\alpha$ is equal to :
Solution:
$a_{n+2} a_{n+1}-a_{n+1} \cdot a_n=2$
Series will satisfy

$ \frac{a_n+\frac{1}{a_{n+1}}}{a_{n+2}}=\frac{a_{n+2}-\frac{1}{a_{n+1}}}{a_{n+2}} $
$=1-\frac{1}{a_{n+1} a_{n+2}} $
$ =1-\frac{1}{2(r+1)} $
$ =\frac{2 r+1}{2(r+1)}$
Now proof is given by
$ =\displaystyle\prod_{ r =1}^{30} \frac{(2 r +1)}{2( r +1)}$
$ =\frac{(1 \cdot 3 \cdot 5 \cdot \ldots \ldots . .61)}{2^{30} \cdot(2 \cdot 3 \cdot \ldots \ldots .31)} $