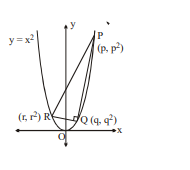
Q.
Consider the parabola $y=x^2$ in the $x y$-plane, with ' $O$ ' as the origin.
Right triangle $PQR$ is inscribed in the given parabola right angle at $Q$, with coordinates as $P ( p$, $p \quad 2$ )
$Q\left(q, q^2\right)$ and $R\left(r, r^2\right)$, where $p, q$ and $r$ are non-zero integers. The value of $\frac{p+r}{q}$, is equal to
Straight Lines
Solution:
$m _{ QP } \cdot m _{ QR }=-1$
$(q+p)(q+r)=-1$. Sum is possible if
$q + p =1$ and $q + r =-1$; on adding $2 q + p + r =0$
$\Rightarrow \frac{ p + r }{ q }=-2$.