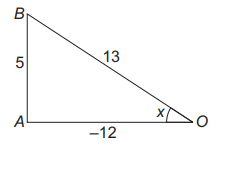
Question

Consider the information given below $\tan x=-\frac{5}{12}$, where $x$ lies in second quadrant.
Statement I The values of $\cot x, \sin x, \cos x$, $\operatorname{cosec} x, \sec x$ are $\frac{-12}{5}, \frac{5}{13}, \frac{-12}{13}, \frac{13}{5}, \frac{-13}{12}$, respectively.
Statement II In second quadrant the value of $\sin x$ and $\operatorname{cosec} x$ are positive.
Choose the correct option.

• A. Statement I is true; Statement II is true; Statement II is a correct explanation for Statement I
• B. Statement I is true; Statement II is true; Statement II is not a correct explanation for Statement I
• C. Statement I is true; Statement II is false
• D. Statement I is false; Statement II is true

Answer 1

Answer: (B)

In second quadrant, $\frac{\pi}{2} < x < \pi$
Here, $ \tan x=-\frac{5}{12}$

$\therefore \cot x=\frac{1}{\tan x}=-\frac{12}{5}$
(since, in second quadrant $\sin x$ and $\operatorname{cosec} x$ are positive)
$\therefore \sin x=\frac{5}{13}, \operatorname{cosec} x=\frac{13}{5}, \cos x=\frac{-12}{13}, \sec x=\frac{-13}{12}$
Alternate Method
$\tan x=-\frac{5}{12}$
Given that, $x$ lies in second quadrant, i.e., $\frac{\pi}{2}< x< \pi$
$\cot x=\frac{1}{\tan x} =-\frac{12}{5} $
Now, $ \sec ^2 x=1+\tan ^2 x =1+\left(-\frac{5}{12}\right)^2$
$=1+\frac{25}{144}=\frac{169}{144} $
$\Rightarrow \sec ^2 x =\left(\frac{13}{12}\right)^2 $
$\Rightarrow \sec x =\pm \frac{13}{12}$
$\because x$ lies in second quadrant, so we take negative sign.
$ \therefore \sec x=-\frac{13}{12} $
$ \Rightarrow \cos x=\frac{1}{\sec x}=\frac{-12}{13}$
Now, $ \tan x=\frac{\sin x}{\cos x} $
$\Rightarrow -\frac{5}{12}=\frac{\sin x}{-\frac{12}{13}}$
$ \Rightarrow \sin x=\frac{5}{13} $
and $ \operatorname{cosec} x=\frac{1}{\sin x} $
$=\frac{13}{5} $
Hence, option (b) is correct.