Q.
Consider the graph of constraints stated as linear inequalities as below
$5 x+y \leq 100 $...(i)
$ x+y \leq 60 $...(ii)
$x \geq 0 $....(iii)
$y \geq 0$...(iv)
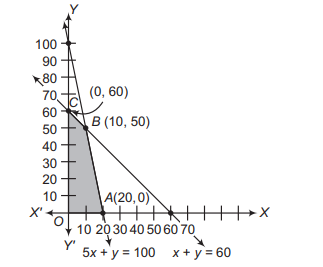
where, $x$ and $y$ are number of tables and chairs on which a furniture dealer wants to make his profit.
The shaded region in the graph is called
Linear Programming
Solution: