Q.
Consider the graph of a cubic polynomial $y=x^3+a x^2+b x+c$ as shown in the figure.
If roots of the cubic equation $x ^3+ ax ^2+ bx + c =0$ are $\alpha, 1, \beta(\alpha, \beta \in I )$ such that $\alpha, 1, \beta$ (in that order) form the first three terms of an arithmetic progression, then find its $5001^{\text {th }}$ term.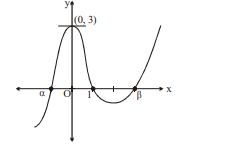
Sequences and Series
Solution: