Question

Consider the functions defined implicitly by the equation $y^3-3 y+x=0$ on various intervals in the real line. If $x \in(-\infty,-2) \cup(2, \infty)$, the equation implicitly defines a unique real valued differentiable function $y=$ $f(x)$.
If $x \in(-2,2)$, the equation implicitly defines a unique real valued differentiable function $y=g(x)$ satisfying $g(0)=0$
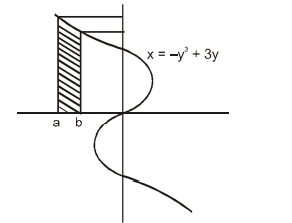
The area of the region bounded by the curve $y=f(x)$, the $x$-axis, and the lines $x=a$ and $x=b$, where $-\infty < a < b < -2$, is

• A. $\int\limits_a^b \frac{x}{3\left((f(x))^2-1\right)} d x+b f(b)-a f(a)$
• B. $-\int\limits_a^b \frac{x}{3\left((f(x))^2-1\right)} d x+b f(b)-a f(a)$
• C. $\int\limits_a^b \frac{x}{3\left((f(x))^2-1\right)} d x-b f(b)+a f(a)$
• D. $-\int\limits_a^b \frac{x}{3\left((f(x))^2-1\right)} d x-b f(b)+a f(a)$

Answer 1

Answer: (A)

$=-a f(a)-(-b f(b))-\int\limits_{f(b)}^{f(a)}-\left(3 y-y^3\right) d y$
$=b f(b)-a f(a)+\int\limits_b^a x f^{\prime}(x) d x$, putting $y=f(x)$
$=b f(b)-a f(a)+\int\limits_b^a \frac{x}{3\left(1-y^2\right)} d x \left(\because \frac{d x}{d y}=3-3 y^2 \equiv \frac{1}{f^{\prime}(x)} \Rightarrow f^{\prime}(x)=\frac{1}{3\left(1-(f(x))^2\right)}\right) $
$ =b f(b)-a f(a)-\int\limits_a^b \frac{x}{3\left(1-(f(x))^2\right)} d x=b f(b)-a f(a)+\int\limits_a^b \frac{x}{3\left((f(x))^2-1\right)} d x$
(1) is correct option
Aliter $\because y^3-3 y+x=0$
So $ y^{\prime}=\frac{-1}{3\left(y^2-1\right)}$
$b f(b)-a f(a)=\mid x \left.f(x)\right|_a ^b=\int\limits_a^b\left\{x f^{\prime}(x)+f(x)\right\} d x$
So area $\Delta=\int\limits_a^b f(x) d x=\int\limits_a^b\left(f(x)+x f^{\prime}(x)-x f^{\prime}(x)\right) d x$
$=x f(x) |_a^b-|x f(x)|_a^b$
$=b f(b)-a f(a)+\int_a^b \frac{x}{3\left(f(x)^2-1\right)} d x$