1. Tardigrade
  2. Question
  3. Mathematics
  4. Consider the function f(x)= begincasesx(x-1) e2 x, text if x ≤ 0 x(1-x) e-2 x, text if x>0 endcases. Then f ( x ) attains its greatest value at

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

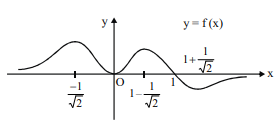
Q. Consider the function $f(x)=\begin{cases}x(x-1) e^{2 x}, & \text { if } x \leq 0 \\ x(1-x) e^{-2 x}, & \text { if } x>0\end{cases}$.
Then $f ( x )$ attains its greatest value at

Application of Derivatives

Solution:

Global maximum at $x=\frac{-1}{\sqrt{2}} ; \quad \because f\left(-\frac{1}{\sqrt{2}}\right)> f \left(1-\frac{1}{\sqrt{2}}\right)$

Solution Image