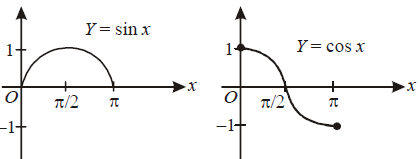Q.
Consider the following statments in S and R
S : Both sin x and cos x are decreasing functions in the interval $\left( \frac{\pi}{2}, \pi \right)$
R : If a differentiable function decreases in an interval (a, b), then its derivative also decreases in (a, b).
Which of the following is true ?
Solution:
From graph it is clear that both sin x and cos x in the interval $(\pi / 2,\pi)$ are decreasing function.
$\therefore $ S is correct.
To disprove R let us consider the counter example :
f (x) = sin x on $(0, \pi / 2)$
so that $f '(x) = \cos x$
Again from graph it is clear that f (x) is increasing on $(0, \pi / 2)$ but $f' (x)$ is decreasing on $(0, \pi / 2)$
$\therefore $ R is wrong.