Question

Consider the following statements
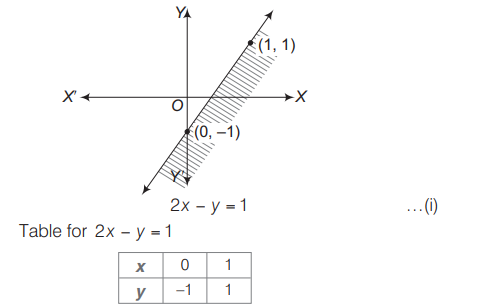
Statement I The graph of the inequality $2 x-y \geq 1$ lies in first quadrant only.
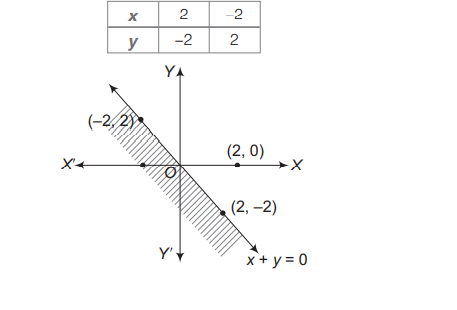
Statement II The graph of $x+y \leq 0$ is

Choose the correct option.

• A. Statement I is true
• B. Statement II is true
• C. Both are true
• D. Both are false

Answer 1

Answer: (D)

I. The line corresponding to given inequality is

Consider the point $O(0,0)$
Since, $ 2(0)-(0) \geq 1$
i.e., $0 \geq 1$, where is not true.
Hence, inequality $2 x-y \geq 1$ represent the half plane made by the line 1 which does not contains origin. Clearly, the graph shows other quadrants are also included.
II. The line corresponding to given inequality is
$x+y=0$ ....(ii)
Table for $ x+y=0$

Consider the point $(2,0)$.
Since, $2+0 \leq 0$.
i.e., $2 \leq 0$ which is not true.
Therefore, $x+y \leq 0$ represent the half plane made by the line $x+y=0$, which does not contains $(2,0)$