Question

Consider the following statements
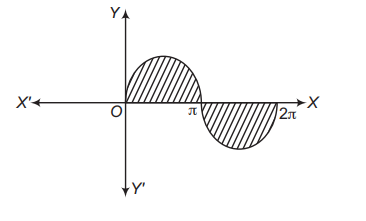
Statement I The area bounded by the curve $y=\sin x$ between $x=0$ and $x=2 \pi$ is 2 sq units.
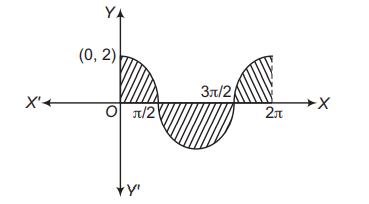
Statement II The area bounded by the curve $y=2 \cos x$ and the $X$-axis from $x=0$ to $x=2 \pi$ is 8 sq units.
Choose the correct option.

• A. Statement $I$ is true
• B. Statement II is true
• C. Both statements are true
• D. Both statements are false

Answer 1

Answer: (B)

I. We have, $y=\sin x$
Let us draw a graph of $\sin x$ between 0 to $2 \pi$.

$\therefore$ Area of shaded region
$ =\int\limits_0^\pi \sin x d x+\left|\int\limits_\pi^{2 \pi} \sin x d x\right|$
$ =[-\cos x]_0^\pi+\left|[-\cos x]_\pi^{2 \pi}\right| $
$ =[-\cos \pi+\cos 0]+|-\cos 2 \pi+\cos \pi| $
$ =|1+1|+|-1-1|$
$ =2+2 $
$ =4 $ sq units
II. We have, $y=2 \cos x$
Let us draw the graph of $2 \cos x$ between 0 to $2 \pi$.

$\therefore$ Area of shaded region
$=\int\limits_0^{\pi / 2} 2 \cos x d x+\left|\int\limits_{\pi / 2}^{3 \pi / 2} 2 \cos x d x\right|+\int\limits_{3 \pi / 2}^{2 \pi} 2 \cos x d x$
$=2[\sin x]_0^{\pi / 2}+\left|[2 \sin x]_{\pi / 2}^{3 \pi / 2}\right|+[2 \sin x]_{3 \pi / 2}^{2 \pi}$
$=2\left[\sin \frac{\pi}{2}-0\right]+\mid 2\left[\sin \frac{3 \pi}{2}-\sin \frac{\pi}{2}\right]+2\left[\sin 2 \pi-\sin \frac{3 \pi}{2}\right]$
$=2+2 \times 2+2$
$=2+4+2$
$=8$ sq units