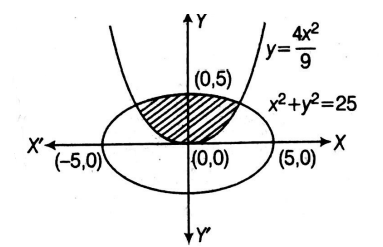
Question

Consider the following relations in the real numbers
$ R_{1}= \left\{\left(x,y\right)\right\} |x^2+y^2\le 25 $ }
$ R_{2 }= \left\{\left(x,y\right)y\ge\frac{4x^{2}}{9}\right\} $
then the range of $ R_1 $ $ \cap $ $ R_2 $ is

• A. [0,5]
• B. [- 3, 3]
• C. [- 5,5]
• D. [-3,5]

Answer 1

Answer: (A)

We have,
$R_{1}=\left\{(x, y), x^{2}+y^{2} \leq 25\right\}$
$R_{2}=\left\{(x, y), y \geq \frac{4 x^{2}}{9}\right\}$
Graph of $R_{1}$ and $R_{2}$ are

Clearly, from graph
range of $R_{1} \cap R_{2}$ is $[0,5]$.