Question

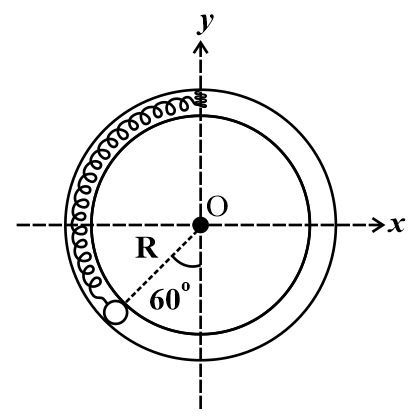
Consider the figure here. A particle of mass $m$ is constrained to move inside a smooth vertical groove of radius $R$ and is connected to a light spring of spring constant $K$ in equilibrium. $O$ is centre of the groove. $x$ and $y$ are horizontal and vertical axes respectively. Different physical parameters are related as $2KR=7mg$ . Angular frequency of the oscillations, if the particle is slightly displaced from the shown equilibrium position is

• A. $\sqrt{\frac{g}{R}}$
• B. $\sqrt{\frac{g}{2 R}}$
• C. $2\sqrt{\frac{g}{R}}$
• D. $\sqrt{\frac{2 g}{R}}$

Answer 1

Answer: (C)

Restoring torque on small displacement $d\theta $
$\tau=KR^{2}d\theta +\frac{m g}{2}Rd\theta $
$\Rightarrow \alpha =\frac{\tau}{l}=\frac{\left(K R^{2} + \frac{m g}{2} R\right) d \theta }{m R^{2}}$
$=\left(\frac{K}{m} + \frac{g}{2 R}\right)d\theta =\left(\omega \right)^{2}d\theta $
$\Rightarrow \omega =\sqrt{\frac{K}{m} + \frac{g}{2 R}}=2\sqrt{\frac{g}{R}}$