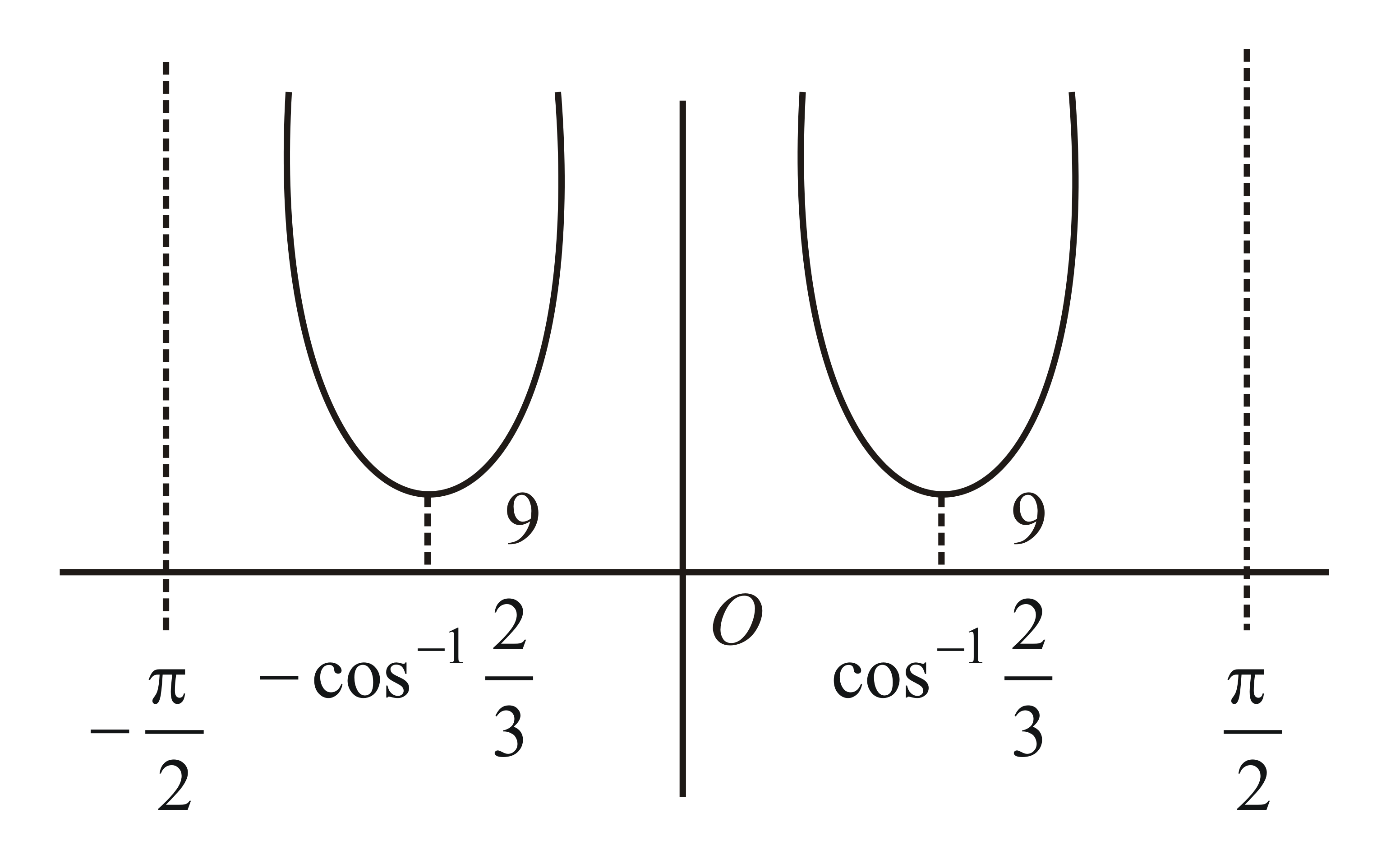Question

Consider the curve $\frac{4}{cos x}+\frac{1}{1 - cos ⁡ x} \, where \, x\in \left(- \frac{\pi }{2} , 0\right)\cup\left(0 , \frac{\pi }{2}\right) \, $ . The value of $a, \, a\in R$ for which the line $y=a$ and the given curve has only one solution is:

Answer 1

Let $t=cos x\in \left(0 , \, 1\right) $ for $ x\in \left(- \frac{\pi }{2} , 0\right)\cup\left(0 , \frac{\pi }{2}\right) $ then $f\left(t\right)=\frac{4}{t}+\frac{1}{1 - t},t\in \left(0 , \, 1\right)$
$f^{1}\left(t\right)=\frac{\left(2 - t\right) \left(2 t - 3\right)}{t^{2} \left(1 - t\right)^{2}}>0 \,$ for $\frac{2}{3} < t < 1 \, $
$ < 0 \,$ for $\, 0 < t < \frac{2}{3}$
$\therefore \, \, $ At $t=\frac{2}{3},f\left(t\right)$ has global minimum value $= 9$
$\therefore \, \, $ Least value of a for which $f\left(t\right)=a$ has solution is $9$