Q.
Consider the circuits shown in the figure. Both the circuits are taking same current from battery but current through $R$ in the second circuit is $\frac{1}{10}$ th of current through $R$ in the first circuit. If $R$ is $11\, \Omega$, the value of $R_{1}$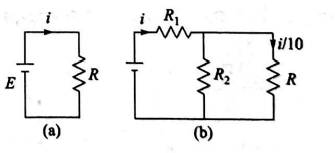
Current Electricity
Solution: