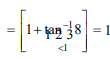Q.
Consider $f(x)=\tan ^{-1}\left(\frac{|x|}{\sqrt{1-x^2}}\right)+\cos ^{-1}\left(\frac{1}{\sqrt{1+x^2}}\right)$
List-I
List-II
P
The number of integer(s) in the range of $f(x)$ is (are)
1
1
Q
The number of solutions(s) of the equation $f(x)=2$ is (are)
2
2
R
The value of $f (\tan 1)$ is
3
3
S
The value of $[ f (\sin 1)]$ is
4
Not defined
[Note: $[ k ]$ denotes greatest integer less than or equal to $k$.]
| List-I | List-II | ||
|---|---|---|---|
| P | The number of integer(s) in the range of $f(x)$ is (are) | 1 | 1 |
| Q | The number of solutions(s) of the equation $f(x)=2$ is (are) | 2 | 2 |
| R | The value of $f (\tan 1)$ is | 3 | 3 |
| S | The value of $[ f (\sin 1)]$ is | 4 | Not defined |
Inverse Trigonometric Functions
Solution:
domain $|x|<1$
$| x |=\sin \theta \text { in } T _1 \theta \in\left[0, \frac{\pi}{2}\right) $
$\therefore T _1=\tan ^{-1} \tan \theta=\sin ^{-1}| x | $
$\text { put }| x |=\tan \theta \text { in } T _2 \theta \in\left[0, \frac{\pi}{2}\right) $
$T _2=\cos ^{-1} \cos \theta=\tan ^{-1}| x | $
$f ( x )=\sin ^{-1}| x |+\tan ^{-1}| x |$
(P) $ \because$ both are increasing function in $| x | \in[0,1)$
$\therefore y \in\left[0, \frac{3 \pi}{4}\right)=\{0,1,2\} \rightarrow \text { Range }$
(Q) when $y=2$ then $|x|=A \Rightarrow x= \pm A$
(R) $ \because \tan 1>\tan \frac{\pi}{4} \Rightarrow \tan 1>1$
$ \therefore f (\tan 1) \text { is ND }$
$\text { (S) } [ f (\sin 1)]=\left[\sin ^{-1}|\sin 1|+\tan ^{-1}|\sin 1|\right]=\left[\sin ^{-1} \sin 1+\tan ^{-1} \sin 1\right]$