Question

$\text { Consider } f ( x )=\begin{cases} \cos x & 0 \leq x <\frac{\pi}{2} \\ \left(\frac{\pi}{2}- x \right)^2 &\frac{\pi}{2} \leq x <\pi \end{cases}$ such that $f$ is periodic with period $\pi$, then

• A. $ \text { The range of } f \text { is }\left[0, \frac{\pi^2}{4}\right)$
• B. fis continuous for all real $x$, but not differentiable for some real $x$
• C. fis continuous for all real $x$
• D. The area bounded by $y=f(x)$ and the $X$-axis from $x=-n \pi$ to $x=n \pi$ is $2 n\left(1+\frac{\pi^3}{24}\right)$ for a given $n \in N$

Answer 1

Answer: (A), (D)

Given $f(x)=\begin{cases}\cos x & 0 \leq x<\frac{\pi}{2} \\ \left(\frac{\pi}{2}-x\right)^2 & \pi / 2 \leq x<\pi\end{cases}$ and $\quad f$ is periodic with period $\pi$
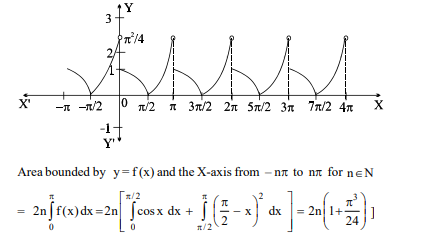
Let us draw the graph of $y=f(x)$
From the graph, the range of the function is $\left[0, \frac{\pi^2}{4}\right) \Rightarrow$(A)
It is discontinuous at $x=n \pi, n \in I$. It is not differentiable at $x=\frac{n \pi}{2}, n \in I$.