Q.
Consider a uniform triangular plate of mass $M$ whose vertices are $ABC$ has lengths $\ell ,\frac{\ell }{\sqrt{2}}$ and $\frac{\ell }{\sqrt{2}}$ shown in the figure. The Moment of Inertia of this plate about an axis perpendicular to the plane of the plate and passing through point $A$ is:
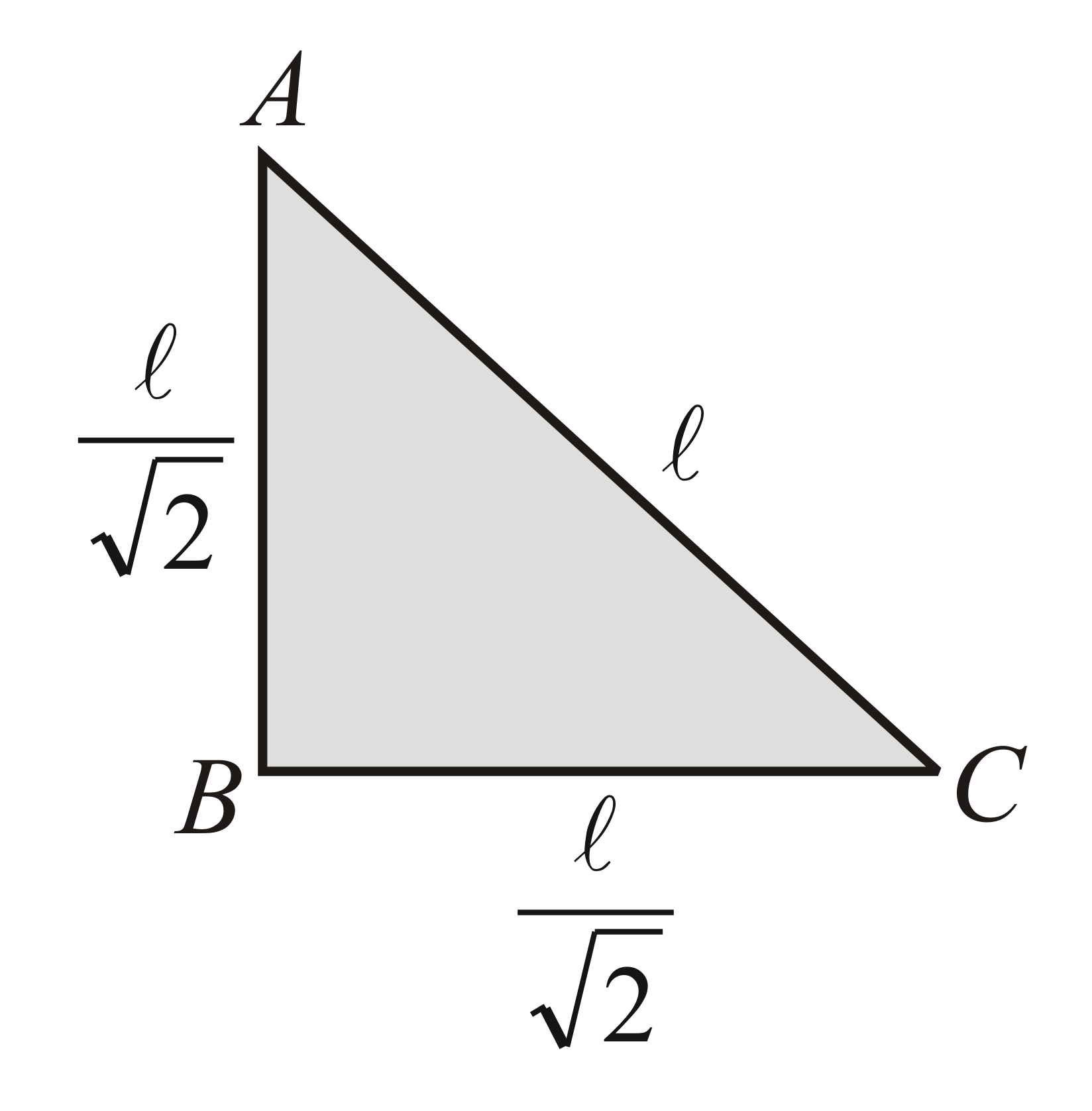
NTA AbhyasNTA Abhyas 2022
Solution:
