Question

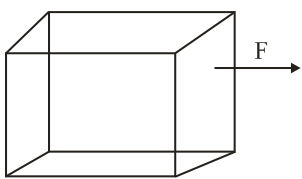
Consider a uniform cubical box of side $a$ on a rough floor that is to be moved by applying minimum possible force $F$ at a point $b$ above its centre of mass (see figure). If the coefficient of friction is $\mu =0.4,$ the maximum possible value of $100\times \frac{b}{a}$ for box not to topple before moving is ________

Answer 1

For no toppling
$F\left(\frac{a}{2} + b\right)\leq mg\frac{a}{2}$
$\mu \frac{a}{2}+\mu b\leq \frac{a}{2}$
$0.2a+0.4b\leq 0.5a$
$0.4b\leq 0.3a$
$b\leq \frac{3 a}{4}$
$b \leq 0.75 a$ (in limiting case)
But it is not possible as $b$ can maximum be equal to $0.5a$
$\left(100 \frac{b}{a}\right)_{max}=50$