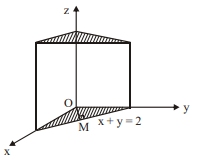
Question

Consider a triangular prism formed by the coordinate planes and planes $P _1: z =4$ and $P _2= x$ $+ y =2$. If $S$ denotes its surface area, $V$ denotes its volume and $d$ denotes the shortest distance between its edge lying in $x y$-plane and $z$-axis, then find the value of $\frac{2 S-5 V}{8 d}$.

Answer 1

$OM = d =\frac{ p +0-21}{\sqrt{2}}=\sqrt{2} $

$\text { Volume }=\frac{1}{2} \times 2 \times 2 \times 4=8 \text { cubic units }$
$\text { Surface area }=2\left(\frac{1}{2} \cdot 2 \cdot 2\right)+4 \cdot 2 \sqrt{2}+4 \cdot 2 \cdot 2=20+8 \sqrt{2} $
$\therefore \frac{2 S -5 V }{8 d }=2$