Q.
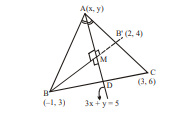
Consider a triangle $ABC$ whose vertices are $B (-1,3)$ and $C (3,6)$. Also the equation of internal angle bisector of $\angle BAC$ is $3 x + y =5$.
The radius of circle circumscribing triangle $ABC$ is equal to
Straight Lines
Solution: