Q.
Consider a toroid with rectangular cross section, of inner radius $a$, outer radius $b$ and height $h$, carrying $n$ number of turns. Then the self-inductance of the toroidal coil when current $I$ passing through the toroid is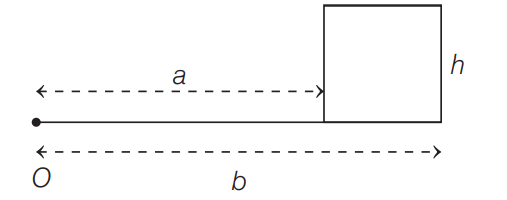
TS EAMCET 2019
Solution:
