Q.
Consider a tank made of glass(reiractive index $1.5$) with a thick bottom. It is filled with a liquid of refractive index $\mu$,. A student finds that, irrespective of what the incident angle $i$ (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of $\mu$ is :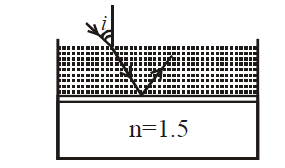
Solution:
$C < i_b$
here $i_b$ is "brewester angle" and c is critical angle
$\sin_{c} <\sin i_{b} $ since $ \tan i_{b} =\mu_{0_{rel }} = \frac{1.5}{\mu}$
$ \frac{1}{\mu } < \frac{1.5}{\sqrt{\mu^{2} + \left(1.5\right)^{2}}} \therefore \sin i_{b} = \frac{1.5}{\sqrt{\mu^{2} + \left(1.5\right)^{2}}} $
$\sqrt{\mu^{2} \times\left(1.5\right)^{2}} < 1.5 \times\mu $
$ \mu^{2} +\left(1.5\right)^{2} < \left(\mu\times1.5\right)^{2}$
$ \mu< \frac{3}{\sqrt{5}} $
$ \text{slab} \mu = 1.5 $