Question

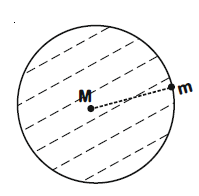
Consider a spherical gaseous cloud of mass density $\rho$(r) in free space where $r$ is the radial distance from its center. The gaseous cloud is made of particles of equal mass $m$ moving in circular orbits about the common center with the same kinetic energy $K$. The force acting on the particles is their mutual gravitational force. If $\rho$(r) is constant in time, the particle number density $n(r) = \rho(r)/m$ is :
[$G$ is universal gravitational constant]

• A. $\frac{K}{\pi r^{2}m^{2}G}$
• B. $\frac{K}{6\pi r^{2}m^{2}G}$
• C. $\frac{3K}{\pi r^{2}m^{2}G}$
• D. $\frac{K}{2\pi r^{2}m^{2}G}$

Answer 1

Answer: (D)

For a particle rotating in the circular orbit of radius r due to the gravitational attraction of inner cloud of mass M,
$\frac{GMm}{r^{2}}=\frac{mv^{2}}{r}$
$\therefore M=\frac{v^{2}r}{G}=\frac{2mv^{2}r}{2Gm}$
As $K=\frac{1}{2}mv^{2}=$ constant, then
$M=\frac{2Kr}{Gm}$ or $dM=\frac{2Kdr}{Gm}$
Correspondingly $dM=\rho\left(r\right)\times4\pi^{2}dr$
$\therefore \rho\left(r\right)\cdot4\pi r^{2}dr=\frac{2Kdr}{Gm}$
$\therefore \frac{\rho\left(r\right)}{m}=\frac{K}{2\pi Gm^{2}r^{2}}$