Q.
Consider a sphere of radius $R$ which carries a uniform charge density $\rho$. If a sphere of radius $\frac{R}{2}$ Ls carved out of it, as shown, the ratio $\frac{\left|\overrightarrow{E_{A}}\right|}{\left|\overrightarrow{E_{B}}\right|}$ of magnitude of electric field $\overrightarrow{E_{A}}$ and $\overrightarrow{E}_{B}$ respectively, at points A and B due to the remaining portion is :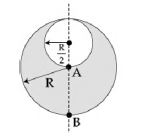
Solution: