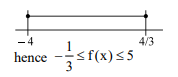Question

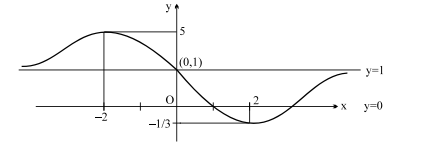
Consider a rational function $f(x)=\frac{x^2-6 x+4}{x^2+2 x+4}$ and a quadratic function $g ( x )=(1+ m ) x ^2-2(1+3 m ) x -2(1+ m )$ where $m$ is a parameter.
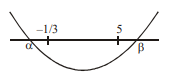
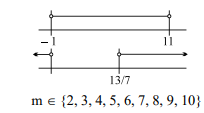
If the range of the function $f(x)$ lies between the roots of $g(x)=0$ then the number of integral values of $m$ equals

• A. 7
• B. 8
• C. 9
• D. 10

Answer 1

Answer: (C)

$f(x)=\frac{x^2-6 x+4}{x^2+2 x+4}=1-\frac{8 x}{x^2+2 x+4}$
$f^{\prime}(x)=-8\left[\frac{\left(x^2+2 x+4\right)-x(2 x+2)}{\left(x^2+2 x+4\right)^2}\right]=-8\left[\frac{-x^2+4}{\left(x^2+2 x+4\right)^2}\right]=\frac{8\left(x^2-4\right)}{\left(x^2+2 x+4\right)^2}$
$f ^{\prime}( x )=0 \Rightarrow x =2 \text { or }-2 $
$f ^{(2)}=\frac{4-12+4}{4+4+4}=\frac{-4}{12}=\frac{-1}{3}$
$f (-2)=\frac{4+12+4}{4-4+4}=5$
Hence range of $f(x)$ is $\left[-\frac{1}{3}, 5\right]$
the graph of $y=f(x)$ is as shown

$\text { Let } y=\frac{8 x}{x^2+2 x+4} $
$x^2 y+2(y-4) x+4 y=0$
$x \in R \Rightarrow D \geq 0 $
$4(y-4)^2-16 y^2 \geq 0 $
$(y-4)^2-(2 y)^2 \geq 0$
$(3 y-4)(y+4) \leq 0$

$f(x)=\frac{x^2-6 x+4}{x^2+2 x+4}=1-\frac{8 x}{x^2+2 x+4}$
$f^{\prime}(x)=-8\left[\frac{\left(x^2+2 x+4\right)-x(2 x+2)}{\left(x^2+2 x+4\right)^2}\right]=-8\left[\frac{-x^2+4}{\left(x^2+2 x+4\right)^2}\right]=\frac{8\left(x^2-4\right)}{\left(x^2+2 x+4\right)^2}$
$f ^{\prime}( x )=0 \Rightarrow x =2 \text { or }-2 $
$f ^{(2)}=\frac{4-12+4}{4+4+4}=\frac{-4}{12}=\frac{-1}{3}$
$f (-2)=\frac{4+12+4}{4-4+4}=5$
Hence range of $f(x)$ is $\left[-\frac{1}{3}, 5\right]$
the graph of $y=f(x)$ is as shown

$\text { Let } y=\frac{8 x}{x^2+2 x+4} $
$x^2 y+2(y-4) x+4 y=0$
$x \in R \Rightarrow D \geq 0 $
$4(y-4)^2-16 y^2 \geq 0 $
$(y-4)^2-(2 y)^2 \geq 0$
$(3 y-4)(y+4) \leq 0$


now $g(x)=0$
$x ^2-\frac{2(1+3 m )}{1+ m } x -\frac{2(1+ m )}{1+ m }=0$
or$g ( x )= x ^2-\frac{2(1+3 m )}{1+ m } x -2=0$
as range of $f(x)$ is $\left[-\frac{1}{3}, 5\right]$
so one root of $g(x)$ is less than $\left(-\frac{1}{3}\right)$ and other is greater than 5
$g \left(-\frac{1}{3}\right)< 0 \text { and } g (5)< 0 $
$g \left(-\frac{1}{3}\right)=\frac{1}{9}+\frac{2}{3} \frac{(1+3 m )}{1+ m }-2< 0=1+\frac{6(1+3 m )}{1+ m }-18< 0=\frac{6(1+3 m )}{1+ m }-17< 0$
$=\frac{6+18 m -17-17 m }{1+ m }< 0=\frac{ m -11}{1+ m }< 0 $
$g (5)< 0$
$25-\frac{10(1+3 m )}{1+ m }-2< 0 ; 23-\frac{10(1+3 m )}{1+ m }< 0 ; \frac{23+23 m -10-30 m }{1+ m }< 0 $
$\frac{13-7 m }{1+ m }< 0 ; \frac{7 m -13}{ m +1} >0$