Question

Consider a rational function $f(x)=\frac{x^{2}-3 x-4}{x^{2}-3 x+4}$ and a quadratic function $g(x)=x^{2}-(b+1) x+b-1$, where $b$ is a parameter.
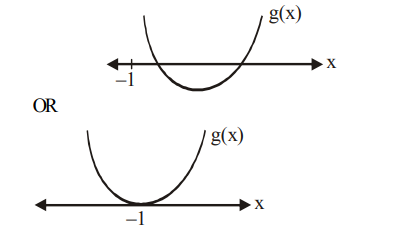
If both roots of the equation $g ( x )=0$ are greater than $-1$, then b lies in the interval.

• A. $(-\infty,-2)$
• B. $\left(-\infty, \frac{-1}{4}\right)$
• C. $(-2, \infty)$
• D. $\left(\frac{-1}{2}, \infty\right)$

Answer 1

Answer: (D)

Different possibilities are as follows :

If both roots of $g ( x )=0$ are greater than $-1$, then 3 conditions should be satisfied simultaneously.
(1) $D \geq 0$
(2) $\frac{-B}{2 A}>-1$
(3) $g (-1)>0$
Now, $(1) \Rightarrow (b+1)^{2}-4(b-1) \geq 0$
$ \Rightarrow b^{2}-2 b+5 \geq 0 \forall b \in R $
$(2) \Rightarrow \frac{b+1}{2}>-1 \Rightarrow b>-3$
and $(3) \Rightarrow 1+(b+1)+(b-1)>0$
$ \Rightarrow b>-\frac{1}{2}$
hence from $(1) \cap(2) \cap(3)$, we get
$b \in\left(\frac{-1}{2}, \infty\right)$