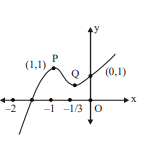
Question

Consider a polynomial $f(x)=x^3+2 x^2+x+1$. Let $P$ and $Q$ denote the point of local maxima and local minima respectively and $O$ is origin, then which of the following statement(s) is/are CORRECT?

• A. Local maximum value of $f(x)$ is unity.
• B. Local minimum value of $f(x)$ is $\frac{23}{27}$.
• C. Tangent of the acute angle between $O P$ and $O Q$ is $\frac{7}{16}$
• D. $f(x)=0$ has a root in the interval $[-2,-1]$

Answer 1

Answer: (A), (B), (C), (D)

$f(x)=1+x(x+1)^2 $
$f^{\prime}(x)=3 x^2+4 x+1=(3 x+1)(x+1)$
$f(-1)=1, f\left(-\frac{1}{3}\right)=1-\frac{1}{3} \cdot \frac{4}{9}=1-\frac{4}{27}=\frac{23}{27} $
$\text { Point } P(-1,1) $
$\text { Point } Q\left(-\frac{1}{3}, \frac{23}{27}\right)$
$m_{O P}=-1, m_{O Q}=-\frac{23}{9}$
$\tan \theta=\frac{7}{16} .$