Q.
Consider a physical pendulum consisting of an inverted "$T$" shaped rigid body made out of two identical, thin, uniform rods of mass $M$ and length $L$ each joined together and hinged at the top point as shown, free to rotate in a vertical plane about an axis perpendicular to the plane of the figure, the time period for 'small' angular oscillations is $T=2 \pi \sqrt{\frac{\alpha L}{\beta g}}$. Find $|\alpha-\beta|$.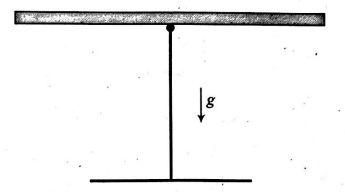
Oscillations
Solution: