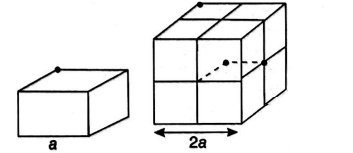
Question

Consider a cube having a uniform volume charge density $\rho$. Find the ratio of electrostatic potential at the centre of the cube to that potential at a corner of the cube.

Answer 1

Consider a uniformly charged cube of side length $a$, and charge density $\rho$.

From dimensional analysis
$V_{\text {corner }} \propto \frac{\rho a^{3}}{a}$
$ V_{\text {corner }} \propto \rho a^{2}$
Now consider a big cube of side length $2 a$
$\frac{V_{\text {comer }}^{\text {Big }}}{V_{\text {comer }}^{\text {small }}}=\left(\frac{2 a}{a}\right)^{2}=\frac{4}{1}$....(i)
But it is clear from the figure that $V_{\text {centre }}^{\text {Big }}=8 V_{\text {Comer }}^{\text {small }}$
$\therefore $ From (i) $ \frac{V_{\text {Comer }}^{\text {Big }}}{\frac{1}{8} V_{\text {Centre }}^{\text {Big }}}=\frac{4}{1} $
$\Rightarrow \frac{V_{\text {Comer }}}{V_{\text {centre }}}=\frac{1}{2}$