Q.
Consider a configuration of $n$ identical units, each consisting of three layers. The first layer is a column of air of height $h=\frac{1}{3} cm$, and the second and third layers are of equal thickness $d=\frac{\sqrt{3}-1}{2} cm$, and refractive indices $\mu_1=\sqrt{\frac{3}{2}}$ and $\mu_2=\sqrt{3}$, respectively. A light source $O$ is placed on the top of the first unit, as shown in the figure. A ray of light from $O$ is incident on the second layer of the first unit at an angle of $\theta=60^{\circ}$ to the normal. For a specific value of $n$, the ray of light emerges from the bottom of the configuration at a distance $l=\frac{8}{\sqrt{3}} cm$, as shown in the figure. The value of $n$ is ______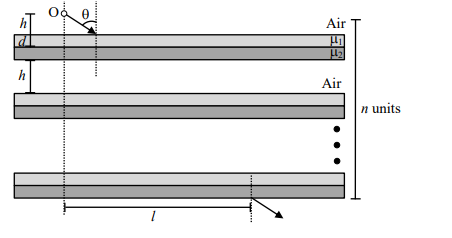
JEE AdvancedJEE Advanced 2022
Solution:
