Question

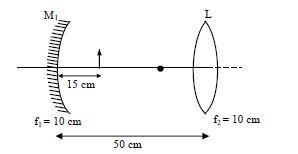
Consider a concave mirror and a convex lens (refractive index = 1. 5) of focal length 10 cm each , separated by a distance of 50 cm in air (refractive index = 1) as shown in the figure. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification $M_1$. When the set-up is kept in a medium of refractive index 7/6, the magnification becomes $M_2$. The magnitude $\left|\frac{M_{2}}{M_{1}}\right|$ is

Answer 1

In vacuum
For mirror $u = - 15, \,f = - 10$
then $\frac{1}{v} +\frac{1}{-15} = \frac{1}{-10}$ (According to mirror formula)
$v = -30$
$m_{1} = - \left(\frac{-30}{-15}\right) = -2$
ie $1^{st}$ image is formed at 30 cm before mirror. Now it will behave as object for lens.
hence for lens u $= - 20,\, f = 10$
$\frac{1}{v} - \frac{1}{-20} = \frac{1}{10}$
$v = 20$
$m_{2} = \left(\frac{20}{-20}\right) = -1$
overall magnification $M_{1} = m_{1}m_{2} = 2$
In vacuum
$\frac{1}{f} = \left(\mu -1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
$\frac{1}{10} = \left(\frac{3}{2}-1\right) \left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
$\frac{1}{R_{1}}-\frac{1}{R_{2}} = \frac{1}{5}$
In medium for lens- $\left(\mu = \frac{7}{6}\right)$
$\frac{1}{f'} = \left(\frac{\frac{3}{2}}{\frac{7}{6}}-1\right) \left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
$\frac{1}{f'} = \frac{2}{7}\times\frac{1}{5}$
$f' = \frac{35}{2}$
there is no change for mirror. hence for mirror
$u = -15,\, f = -10$
then $v = -30$
$m_{1}= -2$
For Lens
$u = -20,\, f = \frac{35}{2}$
$\frac{1}{v} - \frac{1}{-20} = \frac{2}{35}$
$v = 140$
$m_{2} = \left(\frac{140}{-20}\right) = -7$
Overall magnification $M_{2} = m_{1} \,m_{2} = 14$
Now $\left(\frac{M_{2}}{M_{1}}\right) = \frac{14}{2} = 7$