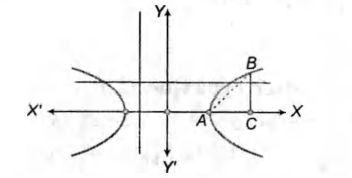
Question

Consider a branch of the hyperbola $x^2 - 2y^2 - 2\sqrt2x - 4\sqrt2y - 6 = 0$ with vertex at the point $A$. Let $B$ be one of the end points of its latusrectum. If $C$ is the focus of the hyperbola nearest to the point $A$, then the area of the $\Delta ABC$ is

• A. $1 - \sqrt\frac{2}{3}$ sq unit
• B. $\sqrt\frac{3}{2} - 1$ sq unit
• C. $1 +\sqrt\frac{2}{3}$ sq unit
• D. $\sqrt\frac{3}{2} + 1$sq unit

Answer 1

Answer: (B)

Given equation can be rewritten as focal chord
$\frac{(x-\sqrt{2})^{2}}{4}-\frac{(y+\sqrt{2})^{2}}{2}=1$
For point $A(x, y), e=\sqrt{1+\frac{2}{4}}=\sqrt{\frac{3}{2}}$
$\Rightarrow x-\sqrt{2}=2 \Rightarrow x=2+\sqrt{2}$

For point $C(x, y), x-\sqrt{2}=\alpha e=\sqrt{6} \Rightarrow x=\sqrt{6}+\sqrt{2}$
Now, $\quad A C=\sqrt{6}+\sqrt{2}-2-\sqrt{2}=\sqrt{6}-2$
and $\quad B C=\frac{b^{2}}{a}=\frac{2}{2}=1$
$\therefore$ Area of $\triangle A B C=\frac{1}{2} \times(\sqrt{6}-2) \times 1=\sqrt{\frac{3}{2}}-1$ sq unit