Question

Column I describes some situations in which a small object moves. Column II describes some characteristics of these motions. Match the situations in Column I with the characteristics in Column II:

Column I		Column II
A	The object moves on the $x$-axis under a conservative force in such a way that its "speed" and "position" satisfy $v =c_{1} \sqrt{c_{2}-x^{2}}$, where $c_{1}$, and $c_{2}$ are positive constants.	P	The object executes a simple harmonic motion.
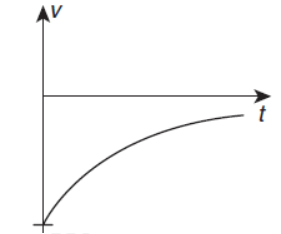
B	The object moves on the $x$-axis in such a way that its velocity and its displacement from the origin satisfy $v=-k x$, where $k$ is a positive constant.	Q	The object does not change its direction.
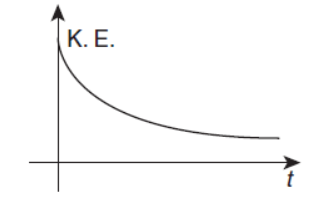
C	The object is attached to one end of a mass-less spring of a given spring constant. The other end of the spring is attached to the ceiling of an elevator. Initially everything is at rest. The elevator starts going upwards with a constant acceleration a. The motion of the object is observed from the elevator during the period it maintains this acceleration.	R	The kinetic energy of the object keeps on decreasing.
D	The object is projected from the earth's surface vertically upwards with a speed $2 \sqrt{G M_{e} / R_{e}}$, where $M_{e}$ is the mass of the Earth and $R_{e}$ is the radius of the Earth. Neglect forces from objects other than the Earth.	S	The object can change its direction only once.

• A. $( A ) \rightarrow( P ) ;( B ) \rightarrow( Q ),( S ) ;( C ) \rightarrow( P ) ;( D ) \rightarrow( Q ),( R )$
• B. $( A ) \rightarrow( P ) ;( B ) \rightarrow( Q ),( R ) ;( C ) \rightarrow( P ) ;( D ) \rightarrow( Q ),( S )$
• C. $( A ) \rightarrow( P ) ;( B ) \rightarrow( Q ),( R ) ;( C ) \rightarrow( P ) ;( D ) \rightarrow( Q ),( R )$
• D. $( A ) \rightarrow( P ) ;( B ) \rightarrow( P ),( R ) ;( C ) \rightarrow( P ) ;( D ) \rightarrow( Q ),( R )$

Answer 1

Answer: (C)

$( A ) \rightarrow( P )$
In SHM, $v=\omega \sqrt{a^{2}-x^{2}}$ which resembles
$v=c_{1} \sqrt{c_{2}-x^{2}}$
and hence the object executes simple harmonic motion.
(B) $\rightarrow(Q),(R)$
We have
$v =- kx =\frac{d x}{d t} \Rightarrow \int \frac{d x}{x}=- k \int dt$
That is,
In $(x)=-k t \Rightarrow x=e^{-k t}$
Therefore,
$v =\frac{d x}{d t}=-k e^{-k t}$
Now,
K.E. $=\frac{1}{2} m v^{2}=\frac{1}{2} m k^{2} e^{-2 k t}$
That is, the object does not change its direction as shown in the following graph:

The kinetic energy keeps on decreasing as shown in the following graph:

$( C ) \rightarrow( P )$
We have $T=2 \pi \sqrt{\frac{m}{k}} ;$
therefore, the motion of the object is SHM.
(D) $\rightarrow( Q ),( R )$
As the object goes up against gravity, its speed and hence the kinetic energy goes on decreasing. Also, since
$V =2 \sqrt{\frac{G M_{e}}{R_{e}}}>$ Escape speed $=\sqrt{\frac{2 G M_{e}}{R_{e}}}$
we conclude that the object cannot return to Earth once again.