Question

Column I		Column II
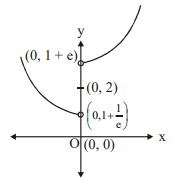
A	Let $f : R \rightarrow R$ defined as $f(x)=e^{\operatorname{sgn} x}+e^{x^2}$, where $\operatorname{sgn} x$ denotes signum function of $x$, then $f(x)$ is	P	Odd
B	Let $f :(-1,1) \rightarrow R$ defined as$f(x)=x\left[x^4\right]+\frac{1}{\sqrt{1-x^2}}$where $[x]$ denotes greatest integer less than or equal to $x$, then $f(x)$ is	Q	Even
C	Let $f : R \rightarrow R$ defined as$f(x)=\frac{x(x+1)\left(x^4+1\right)+2 x^4+x^2+2}{x^2+x+1}$then $f(x)$ is	R	Neither odd nor even
D	Let $f : R \rightarrow R$ defined as$f ( x )= x +3 x ^3+5 x ^5+\ldots \ldots .+101 x ^{101}$then $f(x)$ is	S	One-One
		T	Many-One

• A. (A) R, T ; (B) Q, T ; (C) R, T ; (D) P, P
• B. (A) R, T ; (B) Q, T ; (C) R, T ; (D) P, Q
• C. (A) R, T ; (B) Q, T ; (C) R, T ; (D) P, R
• D. (A) R, T ; (B) Q, T ; (C) R, T ; (D) P, S

Answer 1

Answer: (D)

(A)$f(x)=e^{\operatorname{sgn} x}+e^{x^2}$
when $x=0 f(0)=2$
when $x>0 f(x)=e+e^{x^2}$
when $x <0 f ( x )=\frac{1}{ e }+ e ^{ x ^2}$
Hence, $f(x)$ is many-one and neither odd nor even.
(B) $D_{ f }: 1- x ^2>0 $
$x ^2-1 < 0 \Rightarrow x \in(-1,1) $
${\left[ x ^4\right] \text { when } x \in(-1,1) \text { is equal to } 0 .}$
$\therefore f ( x )=\frac{1}{\sqrt{1- x ^2}}$
Hence, $f(x)$ is even and many-one.
(C) $ f ( x )= x ^4+1+\left(\frac{ x ^4+ x ^2+1}{ x ^2+ x +1}\right)= x ^4+1+ x ^2- x +1= x ^4+ x ^2- x +2= x \left( x ^3+ x -1\right)+2$
Hence, $f(x)$ is many-one and neither odd nor even.
(D) $ f ( x )= x +3 x ^3+5 x ^5+\ldots \ldots .+101 x ^{101}$
Clearly $f(x)$ is an odd function.
Now $f^{\prime}(x)=1^2+3^2 x^2+5^2 x^4+$ $+(101)^2 x ^{100}$.
$\Rightarrow f ^{\prime}( x )>0 \forall x \in R$
Hence, $f(x)$ is one-one function.