Q.
Column I
Column II
A
${ }^{24} C _2+{ }^{23} C _2+{ }^{22} C _2+{ }^{21} C _2+{ }^{20} C _2+{ }^{20} C _3$ is equal to
p
102
B
In the adjoining figure number of progressive ways to reach from $(0,0)$ to $(4,4)$ passing through point $(2,2)$ are (particle can move on horizontal or vertical line)
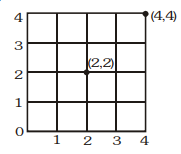
q
2300
C
The number of 4 digit numbers that can be made with the digits $1,2,3,4,3,2$
r
82
D
If $\left\{\frac{500 !}{14^{ k }}\right\}=0$, then the maximum natural value of $k$ is equal to (where $\{$.$\}$ is fractional part function)
s
36
| Column I | Column II | ||
|---|---|---|---|
| A | ${ }^{24} C _2+{ }^{23} C _2+{ }^{22} C _2+{ }^{21} C _2+{ }^{20} C _2+{ }^{20} C _3$ is equal to | p | 102 |
| B | In the adjoining figure number of progressive ways to reach from $(0,0)$ to $(4,4)$ passing through point $(2,2)$ are (particle can move on horizontal or vertical line)  |
q | 2300 |
| C | The number of 4 digit numbers that can be made with the digits $1,2,3,4,3,2$ | r | 82 |
| D | If $\left\{\frac{500 !}{14^{ k }}\right\}=0$, then the maximum natural value of $k$ is equal to (where $\{$.$\}$ is fractional part function) | s | 36 |
Permutations and Combinations
Solution: