Question

Column-1 contains a conic ' $C$ '
Column-2 contains length of latus rectum of conic ' $C$ '
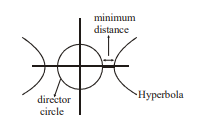
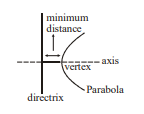
Column- 3 contains the least distance between the conic ' $C$ ' and its director circle

Column I		Column II		Column III
I	$\sqrt{2( x -1)^2+2( y +1)^2}=2\left|\frac{3 x -4 y +1}{5}\right|$	i	$\sqrt{2}$	P	$\frac{1}{5}$
II	$5 y^2-10 y-4 x+1=0$	ii	$\frac{16 \sqrt{2}}{5}$	Q	$\sqrt{2}-1$
III	$\sqrt{( x -1)^2+( y +1)^2}=\left|\frac{3 x -4 y +1}{25}\right|$	iii	$\frac{16}{25}$	R	$\frac{8 \sqrt{2}}{5}$
IV	$x^2-2 y^2-2 x-4 y-3=0$	iv	$\frac{4}{5}$	S	$\frac{2}{15}$

Which of the following is a CORRECT combination ?

• A. (I) (iii) (S)
• B. (II) (iv) (P)
• C. (III) (ii) (S)
• D. (IV) (iv) (Q)

Answer 1

Answer: (B)

(I)$\sqrt{2( x -1)^2+2( y +1)^2}=2\left|\frac{3 x -4 y +1}{5}\right| $
$\Rightarrow \sqrt{( x -1)^2+( y +1)^2}=\sqrt{2}\left|\frac{3 x -4 y +1}{5}\right|$
Focus $(1,-1)$ and directrix $3 x-4 y+1=0$
It represent hyperbola with $e =\sqrt{2}$
ae $-\frac{a}{ e }=$ perpendicular distance from focus to directrix
$a\left(\frac{2-1}{\sqrt{2}}\right)=\frac{8}{5} \Rightarrow a =\frac{8 \sqrt{2}}{5}$
$\Theta b ^2= a ^2\left( e ^2-1\right)$

Length of latus rectum $=\frac{2 b^2}{a}=\frac{2 a^2\left(e^2-1\right)}{a}=2 \times \frac{8 \sqrt{2}}{5}(2-1)=\frac{16 \sqrt{2}}{5}$
Least distance between the conic and its director circle is $\left|\sqrt{ a ^2- b ^2}- a \right|$
$=\left|\sqrt{ a ^2- a ^2\left( e ^2-1\right)}- a \right|=\left| a \sqrt{2 e ^2}- a \right|=\frac{8 \sqrt{2}}{5} .$
(II)
$5 y^2-10 y-4 x+1=0 \Rightarrow 5\left(y^2-2 y+1\right)=4 x+4$
$\Rightarrow 5(y-1)^2=4(x+1) \Rightarrow(y-1)^2=\frac{4}{5}(x+1)$
It represent parabola.
Focus $(-1,1)$, directrix $x+1=\frac{-1}{5}$ (director circle)
$\Rightarrow x=\frac{-6}{5}$
Minimum distance between conic and director circle is $=\left|\frac{-6}{5}-(-1)\right|=\frac{1}{5}$.
(III) $\sqrt{( x -1)^2+( y +1)^2}=\frac{1}{5}\left|\frac{3 x -4 y +1}{5}\right|$
Focus $(1,-1)$; directrix $=3 x-4 y+1$
It represent ellipse with $e =\frac{1}{5}$
$\Theta \frac{ a }{ e }- ae =$ perpendicular distance from locus to directrix
$a \left(\frac{1- e ^2}{ e }\right)=\frac{8}{5} \Rightarrow a =\frac{1}{3}$
$\Theta e ^2=1-\frac{ b ^2}{ a ^2} \Rightarrow b ^2= a ^2\left(1- e ^2\right)$.
Length of latus rectum $=\frac{2 b ^2}{ a }=\frac{2 a ^2\left(1- e ^2\right)}{ a }=\frac{16}{25}$
least distance between conic and director circle is $\left|\sqrt{ a ^2+ b ^2}- a \right|=\left| a \sqrt{2- e ^2}- a \right|$
$\left|\frac{1}{3} \sqrt{2-\frac{1}{25}}-\frac{1}{3}\right|=\left|\frac{1}{3}\left(\frac{7}{5}-1\right)\right|=\frac{2}{15} .$
(IV)$x^2-2 y^2-2 x-4 y-3=0 \Rightarrow\left(x^2-2 x+1\right)-\left(2 y^2+4 y+2\right)=2 $
$\Rightarrow(x-1)^2-2(y+1)^2=2 \Rightarrow \frac{(x-1)^2}{2}-\frac{(y+1)^2}{1}=1$
focus $(1,-1)$
It represents hyperbola.
Length of latus rectum $=\frac{2 b ^2}{ a }=\frac{2(1)^2}{\sqrt{2}}=\sqrt{2}$
Least distance between conic and director circle is $\left|\sqrt{ a ^2- b ^2}- a \right|$
$\Rightarrow|\sqrt{2-1}-\sqrt{2}|=\sqrt{2}-1$