Question

Coloured balls are distributed in three bags as shown in the following table :

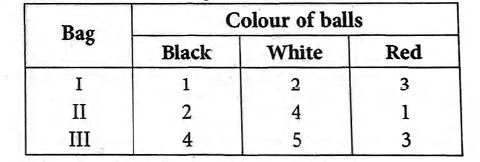
$A$ bag is selected at random and then two balls are drawn from the selected bag. They happen to be black and red. What is the probability that they have come from bag I?

• A. $\frac{231}{551}$
• B. $\frac{232}{551}$
• C. $\frac{233}{550}$
• D. $\frac{231}{550}$

Answer 1

Answer: (A)

Let $E_1$, $E_2$, $E_3$ and $A$ be the events defined as follows :
$E_1 =$ bag $I$ is selected,
$E_2 =$ bag $II$ is selected,
$E_3 =$ bag $III$ is selected and
$A =$ one black and one red ball has been drawn from the selected bag.
As the bags are selected at random,
$P(E_1) = P(E_2) = P(E_3) = \frac{1}{3}$
$P(A|E_1) = $ probability of drawing one black and one red ball when bag $I$ has been selected
$=\frac{^{1}C_{1}\times^{3}C_{1}}{^{6}C_{2}} = \frac{1\times 3}{15} = \frac{1}{5}$
$P(A|E_2) = $ probability of drawing one black and one red ball when bag $II$ has been selected
$=\frac{^{2}C_{1}\times^{1}C_{1}}{^{7}C_{2}} = \frac{2\times 1}{21} = \frac{2}{21}$
$P(A |E_3) = $ probability of drawing one black and one red ball when bag $III$ has been selected
$=\frac{^{4}C_{1}\times^{3}C_{1}}{^{12}C_{2}} = \frac{4\times3}{66} = \frac{2}{11}$
We want to find $P(E_1|A)$
By Bayes' theorem, we have

$P\left(E_{1}|A\right) = \frac{P\left(E_{1}\right)P\left(A |E_{1}\right)}{P \left(E_{1}\right)P\left(A|E_{1}\right) + P\left(E_{2}\right)P\left(A|E_{2}\right)+P\left(E_{3}\right)P\left(A|E_{3}\right)}$
$= \frac{\frac{1}{3}\times\frac{1}{5}}{\frac{1}{3}\times \frac{1}{5}+\frac{1}{3}\times \frac{2}{21}+\frac{1}{3}\times \frac{2}{11}}$
$= \frac{1}{5}\times \frac{1155}{551} = \frac{231}{551}$.