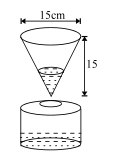
Q. Coffee is draining from a conical filter, height and diameter both $15 cms$ into a cylinderical coffee pot diameter $15 cm$. The rate at which coffee drains from the filter into the pot is $100 cu cm / min$. The rate in $cms / min$ at which the level in the pot is rising at the instant when the coffee in the pot is $10 cm$, is
Application of Derivatives
Solution:
For cylindrical pot
$V =\pi r ^2 h $
$\frac{ dV }{ dt }=\pi\left[ r ^2 \frac{ dh }{ dt }+ h \cdot 2 r \frac{ dr }{ dt }\right] \left( r =\text { constant, } \frac{ dr }{ dt }=0\right)$
hence, $100=\pi r ^2 \frac{ dh }{ dt }$
$100=\pi \cdot \frac{225}{4} \cdot \frac{ dh }{ dt } \left( r =\frac{15}{2} cm \right) $
$\frac{ dh }{ dt }=\frac{400}{225 \pi}=\frac{16}{9 \pi} cm / min$