Question

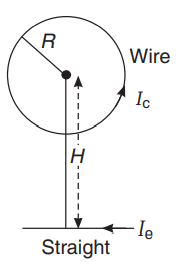
Circular loop of a wire and a long straight wire carry currents $I _{ c }$ and $I _{ e }$, respectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation $H$ is :

• A. $\frac{ I _{ e } R }{ I _{ c } \pi}$
• B. $\frac{ I _{ c } R }{ I _{ e } \pi}$
• C. $\frac{\pi I _{ c }}{ I _{ e } R }$
• D. $\frac{ I _{ e } \pi}{ I _{ c } R }$

Answer 1

Answer: (A)

Magnetic field at the centre $O$ of the loop of radius $R$ is given by
$B _{1}=\frac{\mu_{0} I _{ c }}{2 R }$
where $I_{c}$ is the current flowing in the loop. Magnetic field due to straight current carrying wire at a distance $H$, i.e., at the point $O$ is given by
$B _{2}=\frac{\mu_{0} I _{ e }}{2 \pi H }$
For magnetic field to be zero at the centre of the loop,
$B _{1} = B _{2} $
$\frac{\mu_{0} I _{ c }}{2 R } =\frac{\mu_{0} I _{ e }}{2 \pi H } $
$\Rightarrow H =\frac{ I _{ e } R }{\pi I _{ c }}$