Question

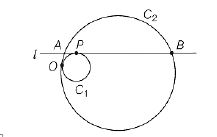
Circles $C_{1}$ and $C_{2}$, of radii $r$ and $R$ respectively, touch each other as shown in the figure. The line $l$ , which is parallel to the line joining the centres of $C_{1}$ and $C_{2}$, is tangent to $C_{1}$ at $P$ and intersects $C_{2}$ at $A, B$. If $R^{2} = 2r^{2}$, then $\angle AOB$ equals

• A. $22 \frac{1^{\circ}}{2}$
• B. $45^{\circ}$
• C. $60^{\circ}$
• D. $67 \frac{1^{\circ}}{2}$

Answer 1

Answer: (B)

Given,

$O'B =R$
$PM=BN=r$
Now, $R^{2}=2r^{2}$
$R= \sqrt{2}r$
$O'B=\sqrt{2}r$
$BN=r$
$\therefore O'N =r$
In $\Delta O' BN$,
$O' N=BN=r $
$\therefore \angle BO'N =45^{\circ}$
Similarly, ${\angle} AO'O=45^{\circ}$
$\therefore {\angle}AO' B=90^{\circ}$
$\Rightarrow {\angle}AOB=\frac{1}{2} {\angle} AO' E$
$\Rightarrow \angle AOB=45^{\circ} $