Q.
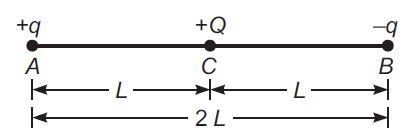
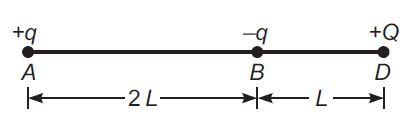
Charges $ +q $ and $ -q $ are placed at points $ A $ and $ B $ respectively which are a distance $ 2 \,L $ apart, $ C $ is the midpoint between $ A $ and $ B $ . The work done in moving a charge $ +Q $ along the semicircle $ CRD $ is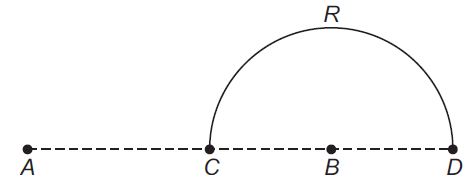
UPSEEUPSEE 2007
Solution: