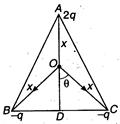
Question

Charges $2q,\, -q$ and $-q$ lie at the vertices of a triangle. The value of $E$ and Vat the centroid of equilateral triangle will be

• A. $ E\ne 0 $ and $ V\ne 0 $
• B. $ E=0 $ and $ V=0 $
• C. $ E\ne 0 $ and $ V=0 $
• D. $ E=0 $ and $ V\ne 0 $

Answer 1

Answer: (C)

The potential due to charge $q$ at a distance $r$ is given by
$V=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}$
Since, potential is a scalar quantity, it can be added to find the sum due to individual charges.
$\Sigma V=V_{A}+V_{B}+V_{C} V_{A}$
$=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{2 q}{x}$
$V_{B}=-\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{x}$
$V_{C}=-\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{x}$
$\therefore V =\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{2 q}{x}-\frac{q}{x}-\frac{q}{x}\right)=0$
Electric field is a vector quantity, hence component along $OD$ is taken
$E=\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{2 q}{x^{2}}+\frac{2 q}{x^{2}} \cos \theta\right) \neq 0$