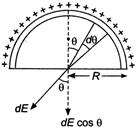
Question

Charge $q$ is uniformly distributed over a thin half ring of radius $R$. The electric field at the centre of the ring is

• A. $\frac{q}{2 \pi^{2} \varepsilon_{0} R^{2}}$
• B. $\frac{q}{4 \pi^{2} \varepsilon_{0} R^{2}}$
• C. $\frac{q}{4 \pi \varepsilon_{0} R^{2}}$
• D. $\frac{q}{2 \pi \varepsilon_{0} R^{2}}$

Answer 1

Answer: (A)

From figure $d l=R d \theta$
charge on $ d l=\lambda R d \theta$
$\left\{\lambda=\frac{q}{\pi R}\right\}$
Electric field at centre due to $d l$ is
$d E=\frac{k \cdot \lambda R d \theta}{R^{2}}$

We need to consider only the component $d E \cos \theta$, as the component $d E \sin \theta$ will cancel out because of the field at $C$ due to the symmetrical element $d l'$
Total field at centre $=2 \int\limits_{0}^{\pi / 2} d E \cos \theta $
$=\frac{2 k \lambda}{R} \int\limits_{0}^{\pi / 2} \cos \theta d \theta $
$=\frac{2 k \lambda}{R} \frac{q}{2 \pi^{2} \varepsilon_{0} R^{2}}$