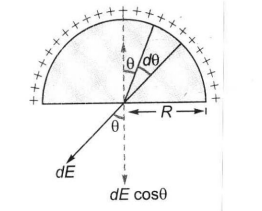
Q. Charge $q$ is uniformly distributed over a thin half ring of radius $R$. The electric field at the centre of the ring is
Electric Charges and Fields
Solution:
From figure di= Rd $ \theta$
charge on dl $ = \lambda R d \theta \bigg \{ \lambda = \frac{ q}{ \pi R } \bigg \} $
E electric field at centre due to di is dE = $ \frac{ k . \lambda R d \theta }{ R^2 } $
We need to consider only the component dE cos $\theta$ , as the component dE sin $\theta$ will cancel out.
Total field at centre = $ 2 \int \limits_0^{ \pi / 2} dE \, cos \, \theta$
= $ \frac{ 2 k \lambda}{ R} \int \limits_0^{ \pi / 2 } cos \, d \theta $
= $ \frac{ 2 k \lambda}{ R} = \frac{ q}{ 2 \pi^2 \, \varepsilon_0 R^2 }$