1. Tardigrade
  2. Question
  3. Chemistry
  4. Calculate the standard cell potential in(V) of the cell in which following reaction takes place: Fe2+(aq)+Ag+(aq)arrow Fe3+(aq)+Ag(s) Given that E°Ag+/Ag =xV E°Fe2+/Fe =yV E°Fe3+/Fe =zV

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. Calculate the standard cell potential in(V) of the cell in which following reaction takes place :
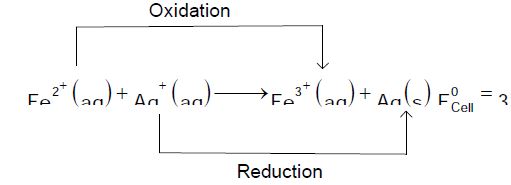
$Fe^{2+}\left(aq\right)+Ag^{+}\left(aq\right)\rightarrow Fe^{3+}\left(aq\right)+Ag\left(s\right)$
Given that
$E^{\circ}_{Ag^{+}}/_{Ag} =xV$
$E^{\circ}_{Fe^{2+}}/_{Fe} =yV$
$E^{\circ}_{Fe^{3+}}/_{Fe} =zV$

JEE MainJEE Main 2019Electrochemistry

Solution:

Given:
$E^{0}_{ Ag'/Ag} = x \quad---- \left(1\right)$
$E^{0}_{ Fe^{2+} /Fe} = y\quad----\left(2\right)$
$E^{0} _{Fe^{2+} /Fe} = z \quad----\left(3\right)$
Using equation:
$\Delta G^{0} = -nFE^{0}$
$\Delta G^{0}_{1} = -fx$
$\Delta G^{0}_{2} = -2Fy$
$\Delta G^{0}_{3} = - 3Fz$
$Fe^{2+} 2e^{-} \to Fe - 2Fy$
$Fe_{_-}^{3+} + 3e_{_-}^{-} \to Fe_{_-} - 3F_{_+}z$
$Fe^{2+} \to Fe^{3+} + e^{-} \left(-2Fy + 3Fz\right)$
$Ag^{+} + e^{-} \to Ag - Fx$
$\Delta G_{Total} = -2Fy+3Fz-Fx = -FE^{0}_{Cell}$
$E^{0}_{Cell} = x+2y-3z$

Solution Image