Question

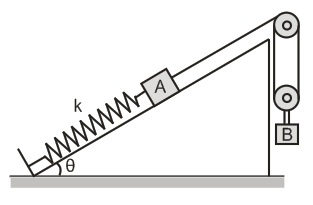
Calculate the angular frequency of the system shown in figure. Friction is absent everywhere and the threads, spring and pulleys are massless. Given that $m_A$ = $m_B$ = m.

• A. $\sqrt{\frac{2 k }{4 m }}$
• B. $\sqrt{\frac{4 k }{5 m }}$
• C. $\sqrt{\frac{6 k }{7 m }}$
• D. $\sqrt{\frac{8 k }{5 m }}$

Answer 1

Answer: (B)

Let $x_{0}$ be the extension in the spring in equilibrium.
Then equilibrium of $A$ and $B$ give,
$T = kx _{0}+ mg \sin \theta \ldots$ (i)
and $2 T = mg \ldots$ (ii)
Here, $T$ is the tension in the string. Now, suppose $A$ is
further displaced by a distance $x$ from its mean position and $v$ be its speed at this moment.
Then $B$ lowers by $\frac{x}{2}$ and speed of $B$ at this instant will be $\frac{v}{2}$ Total energy of the system in this position will be,
$E =\frac{1}{2} k \left(x+ x_{0}\right)^{2}+\frac{1}{2}( m )_{ A }( v )^{2}+\frac{1}{2}( m )_{ B }\left(\frac{ v }{2}\right)^{2}$
$+( m )_{ A }( gh )_{ A }-( m )_{ B }( gh )_{ B }$
or $E =\frac{1}{2} k \left(x +x_{0}\right)^{2}+\frac{1}{2} m ( v )^{2}+\frac{1}{8}( mv )^{2}$
$+ mgx \sin\theta - mg \frac{x}{2}$
or $E =\frac{1}{2} k \left(x+ x_{0}\right)^{2}+\frac{5}{8} m ( v )^{2}+ mgx \sin \theta - mg \frac{x}{2}$
Since, $E$ is constant, $\frac{ dE }{ dt }=0$
or $0 = k \left(x+ x_{0}\right) \frac{ d x}{ dt }+\frac{5}{4} mv \left(\frac{ dv }{ dt }\right)+ mg (\sin\theta )\left(\frac{ d x}{ dt }\right)$
$-\frac{ mg }{2}\left(\frac{ d x}{ dt }\right)$
Substituting, $\frac{ d x}{ dt }= v$
$\frac{ dv }{ dt }=a$ and $k x_{2}+ mg \sin \theta =\frac{ mg }{2}$ [From equations (i) and (ii)]
We get,$\frac{5}{4} m a=- k x$
Since, $a \propto-x$
Motion is simple harmonic, time period of which is,
$T =2 \pi \sqrt{\left|\frac{x}{a}\right|}=2 \pi \sqrt{\frac{5 m }{4 k }}$
$\omega=\frac{2 \pi}{ T }=\sqrt{\frac{4 k }{5 m }}$