Question

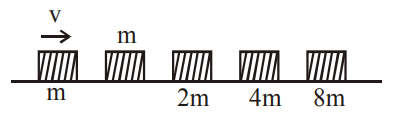
Blocks of masses $m , 2 m , 4 m$ and $8 m$ are arranged in a line on a frictionless floor. Another block of mass $m$, moving with speed $v$ along the same line (see figure) collides with mass $m$ in perfectly inelastic manner. All the subsequent collisions are also perfectly inelastic. By the time the last block of mass $8 m$ starts moving the total energy loss is $p\%$ of the original energy. Value of 'p' is close to :

• A. 77
• B. 37
• C. 87
• D. 94

Answer 1

Answer: (D)

All collisions are perfectly inelastic, so after the final collision, all blocks are moving together
So let the final velocity be $v'$, so on applying
momentum conservation:
$mv =16 m v'$
$ \Rightarrow v ^{\prime}= v / 16$
Now initial energy $E _{ i }=\frac{1}{2} mv ^{2}$
Final energy : $E _{ f }=\frac{1}{2} \times 16 m \times\left(\frac{ v }{16}\right)^{2}$
$\Rightarrow E _{ f }=\frac{1}{2} m \frac{ v ^{2}}{16}$
Energy loss : $E_{i}-E_{f}$
$\Rightarrow \frac{1}{2} mv ^{2}-\frac{1}{2} m \frac{ v ^{2}}{16}$
$\Rightarrow \frac{1}{2} mv ^{2}\left[1-\frac{1}{16}\right] $
$\Rightarrow \frac{1}{2} mv ^{2}\left[\frac{15}{16}\right]$
$\% p =\frac{\text { Energy loss }}{\text { Original energy }} \times 100$
$=\frac{\frac{1}{2} mv ^{2}\left[\frac{15}{16}\right]}{\frac{1}{2} mv ^{2}} \times 100=93.75 \%$
$\Rightarrow $ Value of $P$ is close to $94 .$