Question

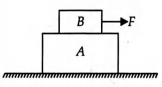
Block $A$ of mass $35\, kg$ is resting on a frictionless floor. Another block $B$ of mass $7 \,kg$ is resting on it as shown in figure. The coefficient of static friction between the blocks is $0.5,$ while coefficient of kinetic friction is $0.4 .$ If a force of $100 N$ is applied to block $B$ acceleration of block $A$ will be (Take $\left.g=10\, m\, s\,{}^{-2}\right)$

• A. $0.8\, m\, s ^{-2}$
• B. $2.4\, m\, s ^{-2}$
• C. $0.4\, m\, s ^{-2}$
• D. $4.4\, m\, s ^{-2}$

Answer 1

Answer: (A)

Here, $m_{A}=35 kg , m_{B}=7 kg , \mu_{s}=0.5, \mu_{k}=0.4$
$F=100\, N , g=10\, m\, s ^{-2}$
Static frictional force on $B$
$f_{s}=\mu_{s} m_{B} g=0.5 \times 7 \times 10=35 N$
As $F>f_{s}$, therefore $A$ and $B$ will move in the same direction
i.e., of applied force, but with different accelerations. Dynamic frictional force on $B$,
$f_{k}=\mu_{k} m_{B} g=0.4 \times 7 \times 10=28 N$
This will oppose the motion of $B$ and cause the motion of $A$.
For $B$, the equation of motion is $F-f_{k}=m_{B} a_{B}$
$\therefore 100-28=7 a_{B} \text { or } a_{B}=\frac{72}{7}=10.3 \,m\, s ^{-2}$
For $A$, the equation of motion is $m_{A} a_{A}=f_{k}$
$\therefore 35 a_{A}=28 \text { or } a_{A}=\frac{28}{35}=0.8 \, ms^{-2}$