Question

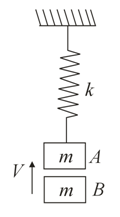
Block $A$ is hanging from a vertical spring and is at rest. Block $B$ strikes the block $A$ with velocity $v$ and sticks to it. Then the value of $v$ for which the spring just attains natural length is :-

• A. $\sqrt{\frac{60 mg^{2}}{k}}$
• B. $\sqrt{\frac{6 mg^{2}}{k}}$
• C. $\sqrt{\frac{10 mg^{2}}{k}}$
• D. $\sqrt{\frac{8 mg^{2}}{k}}$

Answer 1

Answer: (B)

Applying the law of linear momentum conservation, $m v+0=2 mV \Rightarrow V=\frac{v}{2}$
Final $K . E .=\frac{1}{2} \times 2 m \frac{v^2}{2}=\frac{m v^2}{4}$
Applying the law of energy conservation when the spring attains its natural length,
$\frac{m v^2}{4}+0=m g x+\frac{1}{2} k x^2R$
$\because k x=m g $
$\Rightarrow x=\frac{m g}{k}$
$\Rightarrow \frac{m v^2}{4}=m g \times \frac{m g}{k}+\frac{1}{2} k \frac{(m g)^2}{k^2} $
$\Rightarrow \frac{v^2}{4}=\frac{m g^2}{k}+\frac{m g^2}{2 k }$
$\Rightarrow \frac{v^2}{2}=\frac{3 mg ^2}{k} $
$\Rightarrow v=\sqrt{\frac{6 mg ^2}{k}}$