Q.
Average torque on a projectile of mass $m$ (initial speed $u$ and angle of projection $\theta$ ) between initial and final positions $P$ and $Q$ as shown in figure, about the point of projection is: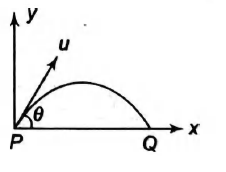
System of Particles and Rotational Motion
Solution: